それではさっそく「ロジックツリー」を利用し、全体を部分に砕いてみましょう。例えば「お金がない」という問題を考えてみましょう。
「お金がない」問題をツリーで整理する
「お金がない」問題は、大まかに考えれば、まずは「お金を稼いでいない」からなのか、「使いすぎている」からなのかという2つの理由に分けられそうです。
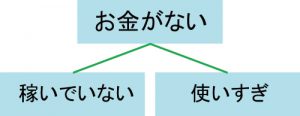
それでは「なぜ、お金を稼いでいない」のでしょうか?
「お金を稼いでいない」問題は「給料=労働時間×時間あたりの給料」ですから、労働時間が短いのが問題なのか、それとも時給が低いのが問題なのかの2つの理由が考えられそうです。
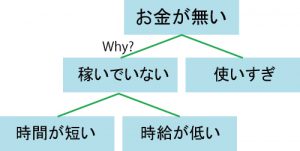
このように「問いかけ」を通じて「順次、選択肢を洗い出す」ことで問題の構造を作る事ができます。お金がない問題をさらに掘り下げていくと、下図のように構造をつくることができます。

こういったツリー構造に問題を整理し分解する図をロジックツリーと呼びます。
うまくツリーをつくるには
いま「問いかけ」を通じて「順次、選択肢を洗い出す」ことで問題の構造を作る事ができると知りました。それでは、どのようにすればうまく構造化ができるのでしょうか?少し手を止めて、考えてみてください。「このようにすれば、うまく構造化できるのではないか」と。
ロジックツリーを眺めていると、ツリーには縦の関係と、横の関係があることがわかります。これら縦と横の関係を正しく定めることで、うまく構造化ができそうです。縦横、それぞれを見ていきましょう。
縦(上下)の関係は、質問と回答の関係
「お金がない」問題の原因を掘り下げた時「なぜお金が無いのか」という質問に対し、下の構造で「稼いでないからでは」「使いすぎだからでは」という回答を行いました。すなわち、縦の関係は質問と回答の関係にあります。

横の関係は、網羅性
例えば「お金がない」問題を構造化するとき、「稼いでない」「使いすぎ」という分解を行いました。ロジックツリーが「整理しながら問題を分解し、構造をつくる」ものだとした時、選択肢(option)を洗い出すという事が大切です。すなわち、横の関係では、網羅性が重要なのです。

今回であれば「それだけなの?」とさらに問うことで、「(そもそも)貯金が無い」からお金が無いのだ、という別のオプションが見つかったりします。
すなわち、縦の関係で問われた「Why?」「How?」という疑問に対し、できるだけ余すことなく答えていくのが横の関係です。
それでは、次章より、縦・横の関係について、より詳細に見ていきましょう。

