「分析」をうまく行うためには、その限界を知っておくことが大切です。ここでは、分析の限界と題し、その分析の限界、その理由、および、対処法を探ります。
それではここで、「分析:分けて考える手法」の問題点や限界を、考えてみてください。
分析と複雑さ
分けて考える – 分析する – のは何のためでしょうか? どうして、分析することが必要なのでしょうか?
それは、分けると、複雑さが減るから、簡単になるからです。科学というのは、一つには分割による単純化を目指しました。
科学の限界:要素の数と複雑さ
科学には限界があります。その限界というのは、1. 要素数の多寡, 2. ランダム性の大小によって規定されます。どういう事でしょうか?
要素が多すぎると、解けない
まず、ランダム性が少ないものについて考えます。身の回りの自動車や、鞄などの製品を見てみてください。どんなものも、『相互作用する』要素の数は~数個と少ないはずです。机の脚の1本は、机の板とはくっついて居ますが、逆側の脚とは相互作用しません。車のタイヤも、車軸に影響を及ぼしますが、車のボディには影響を与えません。これは、相互作用する要素数が多くなればなるほど、計算量が多くなるからです。
具体的には、N 個の要素があるとき、その全てが相互作用するなら $ N^2 $ 個の「関係性」を考えなくてはいけません。これを、計算量二乗の法則と言います。
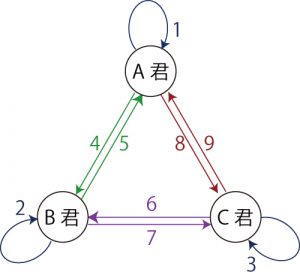
具体的にA 君、B 君、C 君の3人で見てみましょう。まず、A 君自身、B 君自身、C 君自身について考えると3つ考えなくてはいけません。さらに、
- A 君からB 君、B 君からA 君、
- B 君からC 君、C 君からB 君、
- C 君からA 君、A 君からC 君、
の6つの関係があるので、3+6 = 9 つの関係を考えなくてはなりません。
この関係性を表す図を、もう少し簡単に表形式で書き直してみましょう。*1
| A | B | C | |
|---|---|---|---|
| A | A → A | A → B | A → C |
| B | B → A | B → B | B → C |
| C | C → A | C → B | C → C |
上記のように書き表せば、要素がN 個あるとき、その関係性は $ N^2 $ 個という言葉の意味がはっきりと分かって頂けるのでは無いでしょうか?
より具体的には、A → B に3、B → A に1 の「影響」があり、その他は影響が無いとき、以下のように書きます。
| A | B | C | |
|---|---|---|---|
| A | A | 3 | 0 |
| B | 1 | B | 0 |
| C | 0 | 0 | C |
このように、要素の数が大きくなればなるほど、指数的に計算は大変になるのです。相互作用の数が小さければ小さいほど、その物体の振舞いは認識しやすく、容易になります。
ランダムでも、数が大きければ:
次に、ランダムな物体を考えてみましょう。高校物理を習った人は、例えば、気体の分子ひとつひとつがランダムなふるまいをする事を知っていると思います。あるいは、人の寿命を見ても、ある人がいつ死ぬかは、かなりランダムである事が見てとれると思います。
この時、ランダムなもの1つ1つについて考えても、正しい答えは出ません(だからランダムなのですよね)。しかし、ランダムな物体がいくつも集まると、その構成要素1つ1つはランダムでも、全体として何か規則性や、安定性を持つことがあります。これが大数の法則というやつです。
あなたがいつ事故に遭うか、あなたがいつ死ぬかを予測する事は難しく、大変です。ですが、一年間に日本人が何人くらい事故を起こすか、一年間に何人の日本人が死ぬか、という事を考えれば、せいぜい $ \frac{1}{10} ~ \times 10 $ の間で予測がつきます(気体分子の法則もそうですね)。
すなわち、
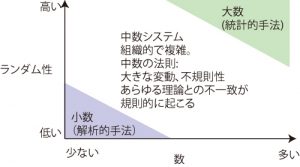
ランダム性が小さい時で、数が少ない時、1つ1つの振舞いを予測できる。
ランダム性が大きい時でも、数が多ければ、全体としての振舞いを予測できる。
前者を小数システムと呼び、後者を大数システムと呼びます。そして、その中間の部分:ランダム性があって、数がそれほど多くない=中数システムこそが我々の住む世界で、それらは科学の予測の範疇外なのです。
それは、下図のようになります。
中数システム:ダイエットの話
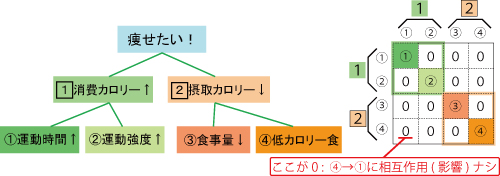
テーマは、ダイエットです。「どうすれば痩せる事ができるのか?」構造化をしてみましょう。はじめに「痩せる行動案」を「消費カロリーを増やす」と「摂取カロリーを減らす」で分割できそうです。つまり、食べ物のカロリーを減らして、運動をすればよい、と。
運動は面倒くさいので、食べ物のカロリー制限だけを実施することにしました。しかし、実際にこれを実践して、一か月も経てば、きちんと記録を取っていると「おかしい」事に気づく人が居ます。摂取カロリーは減らしているし、運動も前より減らしていないのに、痩せないのです。これは、実は「食べるモノ」と「消費カロリー」の間に相互作用があるのが原因です。
消費カロリーの多くは、何も特別な運動をしなくても生じる「代謝」に依ります。その代謝はある程度「食べ物の質」に依存します(ある栄養学の教授によると、タンパク質:脂肪:糖分=20:23:57になるのが理想だそうです)。従って、脂肪を減らしすぎたり、糖質を減らしすぎたりする事で、代謝まで落ちてしまうそうです(具体的には、脂肪を減らすと脂溶性ビタミンの吸収が悪くなり、代謝が落ちる。糖質を減らしすぎると飢餓状態と判断し、内分泌系が代謝を落とす、らしい)*2。
上記の話の真偽はともかく、ここでのポイントは「相互作用」が存在した為に、切り分けたはずのものがその実、上手く切り分けられていなかったということです。
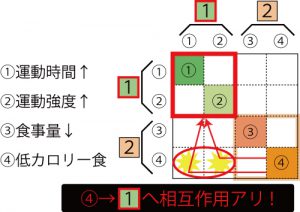
うまく切り分けるためには、この「相互作用」が無いか、無視できるくらい小さな状態が望ましい。
相互作用 [4]
相互作用がゼロあるいはほとんど無いような分割ができたとしたら、それはいい分割です。つまり、下図のような、*3ものが良い分割です。
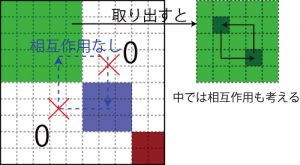
多くの場合は、ここまで綺麗な分割はできません。だから、「できるだけ独立な見方はできないか」「もっとシンプルな見方はできないか」「もっと不確実さを抑えられないか」という思考が重要です(難しかったですね。次に行きましょう、次!)。
*1 本当は行列表示なのですが、簡単のため表で整理します。
*2 本当ですか?医学科・栄養学科の人HELP!
*3 理系で数学に強い人は、この図をN 個のノードを持つネットワークを可視化した行列と見て、色を塗っていない部分以外の成分ゼロ成分だと思ってください

