推定方法について
答えの正確さ
答えの大きさは「正解」の $ \frac{1}{10} ~ \times 10 $ に収まれば良い。
問題を構成要素に分割する
「正解」の $ \frac{1}{10} ~ \times 10 $ だったら当て推量でも当りそうですが、現実に欲しいデータは、そう簡単には行かない場合が多いです。そこで、この推測なら $ \frac{1}{10} ~ \times 10 $ と言えるくらい、細かい構成要素へ問題を分割し
てしまいましょう。
平均は、対数で取る
ある小問題の答えが、例えば、「車の上に人は何人乗れるか」という問題に対して「4人は絶対乗れる」「40人はまず乗れないだろう」という推測をしたとします。それでは、間を取れば良い推測ができそうです。では、どのように間を取ればいいのでしょうか?
答えは、「対数の平均を取る」です。対数の平均とは、数値A と数値B があったとき、 $ \sqrt{A \times B} $ を言います。相乗平均とも言います。
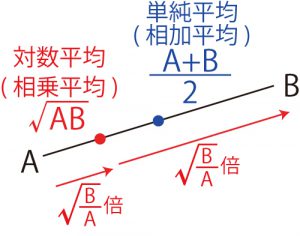
具体的には、4人と40人の「単純平均(相加平均)」は $ \frac{4 + 40}{2} = 22 $ ですが、「対数の平均」を取れば、 $ \sqrt{4 \times 40} = \sqrt{160} \fallingdotseq 13 $ 人という事になります。ルートの計算が綺麗な例では、4人と16人の対数平均であれば、 $ \sqrt{4 \times 16} = \sqrt{64} = 8 $ 人となります。
対数の平均を取るのは、 $ \frac{1}{10} ~ \times 10 $ に収める、という目標に対して、「何倍」であるかが重要だからです。
例えば、1個と100個の単純平均は50.5個ですが、これは最小値1 の50倍。最大値100 の半分でしかありません。しかし、対数平均である $ \sqrt{100} = 10 $ では、10 は最小値1 の10倍、最大値100 は10 の10倍と、「倍率に関して等間隔」である事がわかります。
実用上は、「かけてルート」と覚えるといいでしょう。
問題:本は毎年何冊売れているか?
それでは、これらの「情報収集前の仮説」「数値の推定」を具体的な例で見てみましょう。
「日本国内で、本は毎年何冊売れているか、推定せよ」という問題があったとしましょう。まず情報収集をはじめると、Google で「書籍数年間」などといったキーワードで検索することになると思います。もちろん、それで答えが見つかる可能性はあります。ですが、それでは頭を使っている事にはなりません。それでは、どうすれば良いのでしょうか?
まずは、問題を深堀りし、自分なりに定義してしまいましょう。「言葉に注目して掘り下げる」と、本・売れてるという2つのキーワードが眼に飛び込んできます。では、本というのは何なのでしょうか?小説だけでいいのでしょうか?漫画を入れても良いのでしょうか?雑誌や、新聞は入るのでしょうか?写真集、洋書、理工書はどうでしょうか?
問題には書かれて居ないので、出題者の意図や置かれた状況を推定して、自分なりに決めてしまいましょう。ここでは、雑誌や漫画も含め、「読み物」「実用」「趣味」としての本のうち、個人消費のもの(つまり、大学や図書館などを除くもの) を推定してみましょう。
次に「売れている」という言葉に着目すると、書店の数と年間の1書店あたりの売り上げ冊数から計算できそうです。また、視点を変えて、売れている冊数=買っている冊数のはずですから、日本に居る人の数と、1人あたりの読書量がわかればよさそうです。こちらで考えてみましょう。
日本人全体の、何割くらいが本を「よく読む」のでしょうか? 高校の頃を考えてみると、40人クラスで、読書家1人、というのは少なすぎる気がしますし、20人、というのは多すぎる気がします。(対数の) 間をとって、4人。1割くらいが本を良く読み、9割くらいが本をあまり読まないのでは無いか、という推定をします。
本を良く読む人でも、一日2冊(一週間に14冊) はかなり多い方だと思いますが、一週間に1冊だと、もはや「良く読む」とは言えないでしょう。(対数の) 平均をとって、一週間に3冊程度読む、と推定しましょう。これは、年間150冊程度です。
次に、本をあまり読まない人たちは、一冊も読まない人から、多くても週1冊読む、と推定しましょう。週1冊は年間50冊ですから、年間1冊読む人との間をとって、年間7冊としましょう。
すると、下図のように整理できます。
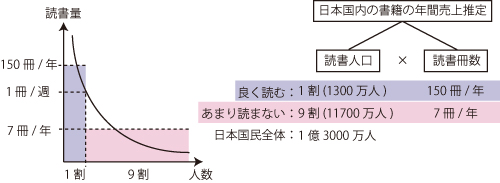
計算すると 1300万 × 150 + 11700万 × 7 = 195000万 + 81900万 = 27億6900万冊 すなわち、約28億冊という推計ができます。
この推計はどのくらい正しいのでしょうか?
統計局の家計における教養娯楽関係費 [65] によると、平成19年度の「書籍・他の印刷物に対して」の2人以上世帯あたり支出は、平均年間52,015円です。日本の世帯数は約5000万で、単独世帯数は1500万ですから、 3500万世帯 × 5.2万円 = 1兆8200億 が、単独世帯を除く、1億3000万人 – 1500 万人 = 1億1500万人 が消費する本の値段の総計です。
人数に比例すると考えると、 $ 1兆8200億 \times \frac{1億3000万人}{1億1500万人} = 約2兆円 $
では一冊あたりの本の値段は幾らくらいでしょうか? 安くて文庫本が500円、普通に買う本は、高くて3000円。約1000円くらいでしょうか。
2兆円 ÷ 1000円 = 20億冊、という事で、「正解」の $ \frac{1}{10} ~ \times 10 $ には納まっていそうです。(統計データを捏ねくり回した「正解」の方が難しいと思いませんか?)
分割して両方考えるとき、片方だけ考えるとき
今、本を「良く読む」「あまり読まない」の2種類のグループに分け、両方を考えました。実は、両方を考えた方が良い時と、片方だけで良い時の2パターンがあります。いったい、どんな時でしょうか?
答えは、「それは重要か?」という問いにあります。簡単に言えば、最終結果にほとんど結果を及ぼさないようなグループは、考えなくても良い、という事です。
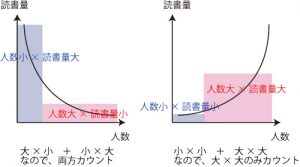
下図のように、大×小と小×大の場合は、両方カウントし、小×小と大×大の場合は、大×大だけ考えればいい(だって、小×小は結果に影響を及ぼさない!) ということになります。「重さ」による判断というわけです。
汝自身を知れ
このように、調べるべき情報を特定したり、「今何が分からないかを明らかにする」ことで、仕事や学習の質や速度を、大幅に上げる事ができます。調べるためには、自分が何が知りたいかを、知らなくてはならないわけです。
例えば、何かのアウトプットを出して、誰かからフィードバックを貰うときにも、自分なりに論点に対する仮説をたて「この点についてフィードバックを下さい」というようにするだけで、優れたフィードバックがもらいやすくなります。すなわち「何が原因で自分が決められないのか」「何に対して不安を感じているのか」を明らかにするわけです。
他にも、研究を行う場合にも、「どういう問題の解決をしたいのか」「その為に、何のデータが必要か」「そのデータは、どのようにして取ればよいか」というように考えてからデータを取るといった仮説志向型アプローチと、何も考えずに全てのデータを取って、それからエクセルや統計ツールで分析して何かを見つけ出そう、というアプローチでは、大きく、大きく違います。

